• Download home

• arb

• Electrokinetic flow solver

arb finite volume solver

Dalton Harvie

New version 0.4 uploaded (19/4/13).

What is arb?

arb is a software package designed to solve arbitrary partial differential equations on unstructured meshes using an implicit finite volume method. The primary strengths of arb are:

• All equations and variables are defined using `maths-type' expressions written by the user, and hence can be easily tailored to each application;
• All equations are solved simultaneously using a Newton-Raphson method, so implicitly discretised equations can be solved efficiently; and
• The unstructured mesh over which the equations are solved can be componsed of all sorts of convex polygons/polyhedrons. One, two and three dimensional domains can be used (simultaneously).

arb is open-source software that is released under the GNU General Public License (GPL). The copyright of arb is held by Dalton Harvie.

Some examples

A diffusion problem:

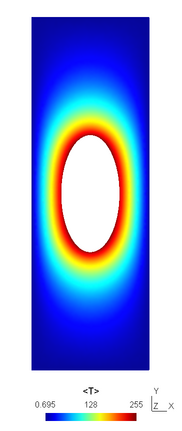
The image (right) shows the solution to the following diffusion problem solved over a 2D domain:

This set of equations is represented by the following in arb:

Four variables are defined: the unknown temperature field, and three equation variables. The equations are satisfied when the equation variables equal zero. Operators are used to express the vector equations using the finite volume method: For example, celldiv performs a divergence around a cell element and facegrad calculates the gradient of a quantity relative to a face element.

This problem is included with the arb distribution. You can browse the arb input file here.

Steady-state flow around a cylinder:

The two-dimensional flow around a cylinder is a CFD benchmark test problem. Here the Reynolds number based on the cylinder diameter and maximum velocity is 20, producing steady-state results.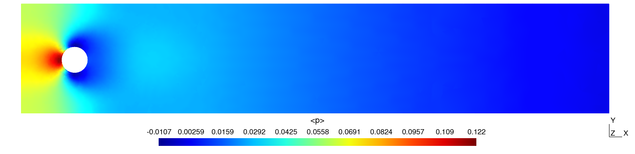

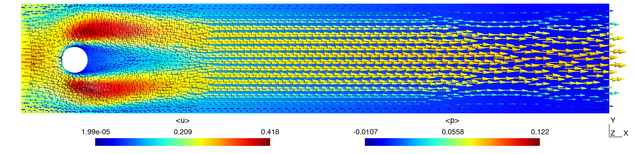
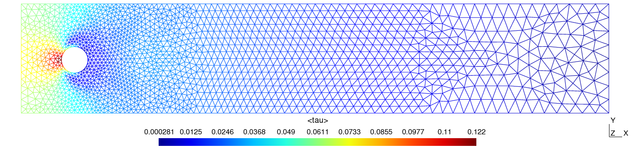
This problem is also included with the arb distribution. You can browse the arb input file here.

What is needed to run arb?

In terms of coding content arb consists of fortran 95, perl and shell scripts. arb requires a UNIX type environment to run, and has been tested on both the Apple OsX and ubuntu linux platforms.

arb depends on certain third party programs and libraries, including:

• A fortran compiler; the Intel compiler ifort or GNU compiler gfortran;
• The computer algebra system maxima;
• A sparse matrix linear solver: UMFPACK, pardiso (included with ifort) or a Harwell Subroutine Library routine; and
• The mesh generation and post-processing package gmsh.

By combining gfortran with the UMFPACK sparse linear solver, arb can be run using freely available GPL licensed software.

Try it out

Getting up and running is straightforward.

On recent versions of ubuntu (tested on 10.04 and 12.04) the following commands will download all the necessary software, run a test simulation and visualise the results:

Installation on OsX takes a bit more time and is detailed in the manual. The procedure is known to work on OsX 10.6 and previously I had it working on OsX 10.4.

Further details for both platforms can be found in the manual.

Download

A tar file containing the latest arb source is here. Older versions can be found in this directory.

Citing

If you use arb to conduct research, please cite it using the publication given below. I am keen to hear of your experiences using arb and also of any feature requests that you have and bugs that you find - drop me an email with `arb' in the subject line.

Where is arb going?

arb is under active development, although updates to this website have not occurred regularly. Previously the major focus was on developing the language feature set - I expect that the application of arb to different types of problems (in particular multiphase and non-Newtonian flows) will become the next development focus. For a summary of the development history and the roughly planned direction see this file.

Publications